Flat Geometry Shapes (English version at the end)
Os presento una Situación de Aprendizaje para llevar al aula con vuestros alumnos. Para ello, hemos diseñado un robot especial que dibuja líneas sobre una pizarra blanca. Tambien puede hacerse sobre papel una vez terminado el diseño.
Adaptando las explicaciones y la dificultad, se puede trabajar desde 5º de primaria hasta 2º de la ESO.
Este robot tiene la particularidad de que sostiene entre sus ruedas delanteras un rotulador de 12mm de diámetro que a la vez que avanza, va dibujando. El rotulador debe ir suelto, es decir, el robot solo lo sostiene derecho, pero debe poder moverse en vertical, para que pueda ir pintando.




Instrucciones de Montaje del robot. Instructions
No hace falta descargarlo, se puede usar online picando en el nombre “cajapintor”
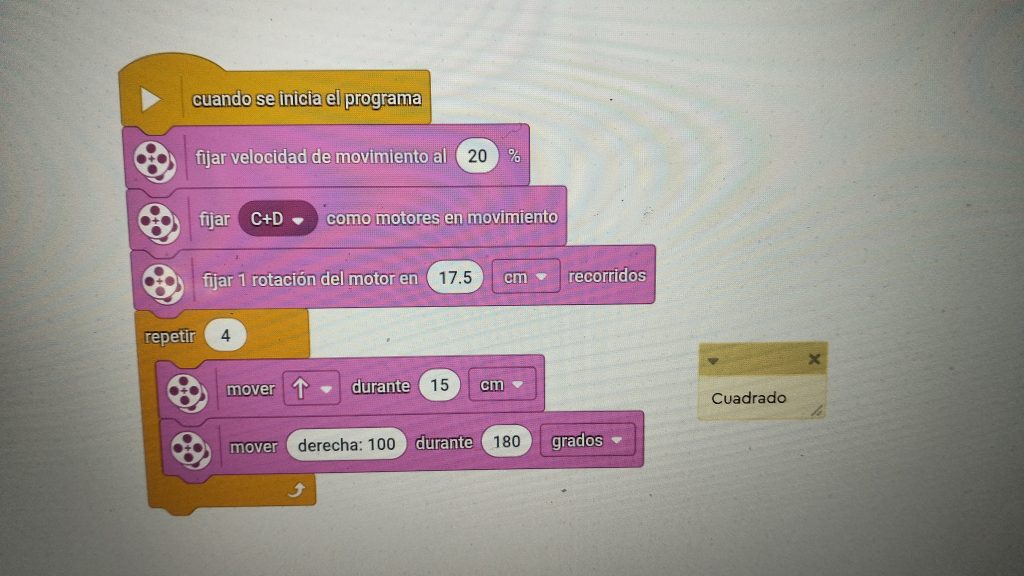
Dibujando un cuadrado
Imaginemos a las figuras como rotondas. El robot debe hacer el giro exterior, como si fuera un coche cambiando de calle, con lo que el ángulo de giro, no es el ángulo de la figura, sino el suplementario.
En las figuras geometricas, las sumas de sus ángulos han de sumar (n – 2 ) x 180º, pero nosotros no buscamos el ángulo interior, sino el suplementario.
El suplementario de un cuadrado (que tiene 4 lados) sería: 360º/4 lados = 90º.
Recordamos a nuestros alumnos que el ángulo de giro de un motor (de una rueda) no es lo mismo que el giro de un robot completo. Cada rueda tiene un ángulo de giro. En este caso, una rueda va hacia adelante 90º y la otra otros 90º , con lo que sumamos 90 + 90 = 180º. Que es lo que ponemos en nuestro código.

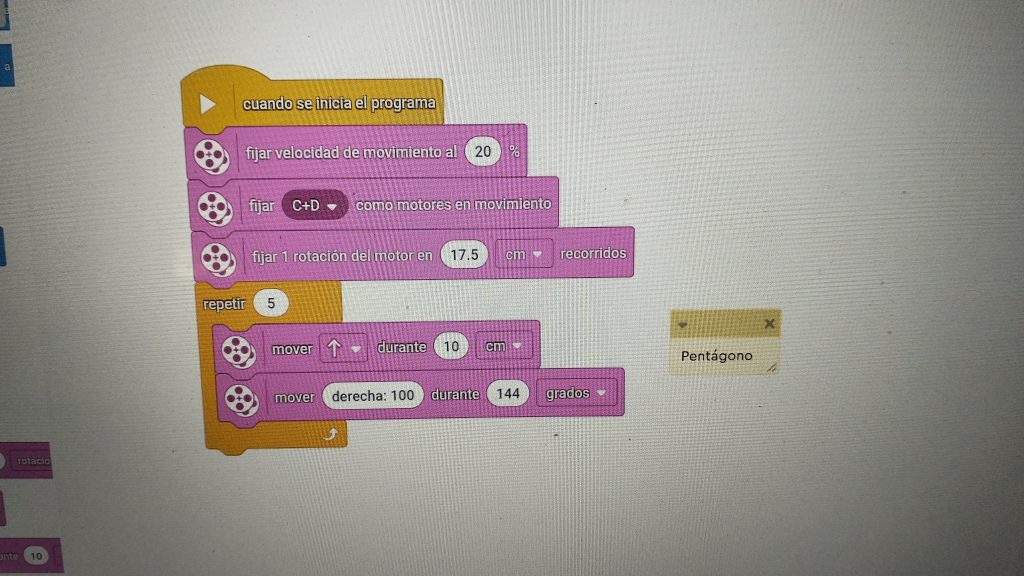
Dibujando un pentágono
Para calcular los ángulos suplementarios de un pentágono, que tiene 5 lados, haríamos así: 360º/5 lados = 72º. Como tenemos que girar 2 ruedas, duplicamos esa cantidad 72º x 2 = 144º.

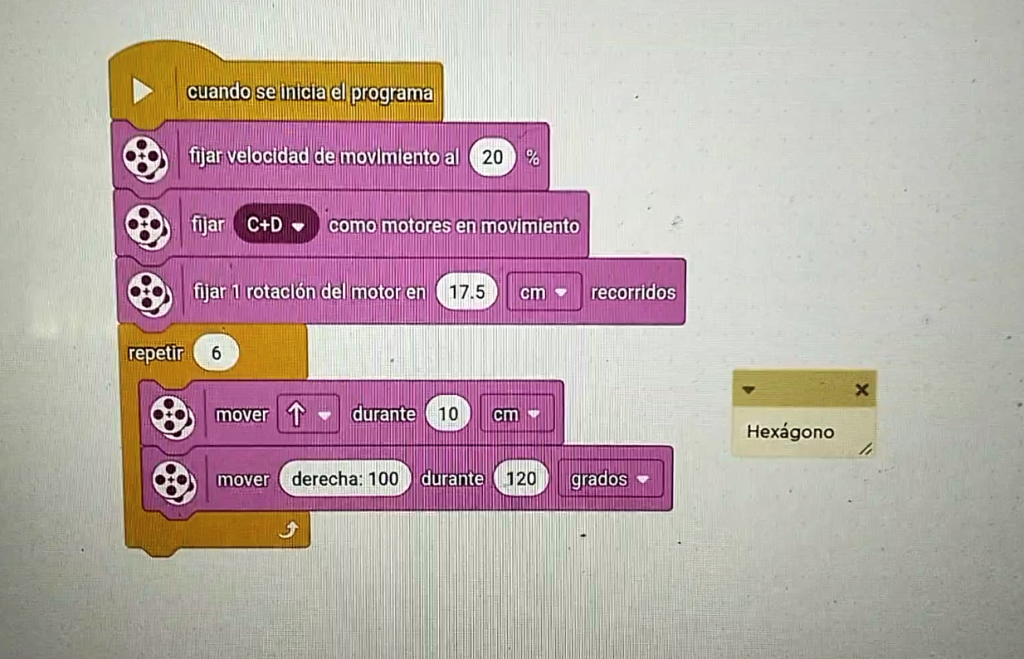
Dibujando un hexágono
Un hexágono tiene 6 lados. Siguiendo ya con lo aprendido, solamente hacemos la operación 360º / 6 lados = 60º. Como son dos motores, debemos poner 60º x 2 = 120º.

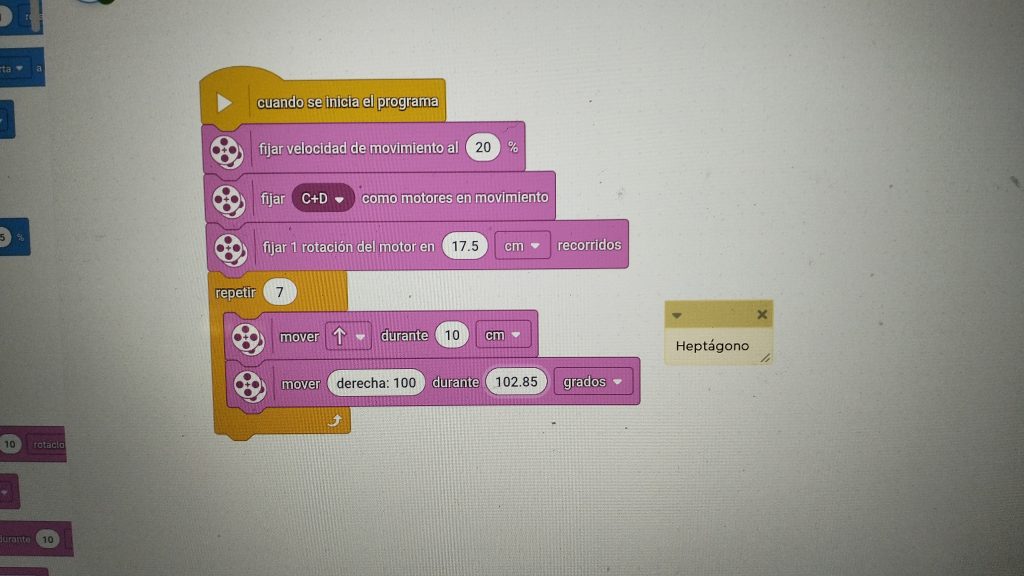
Dibujando un heptágono
En esta figura se complica un poco, ya que la división no es exacta 360º / 7 = 51,42º. Multimplicando por 2 nos da 102,85º

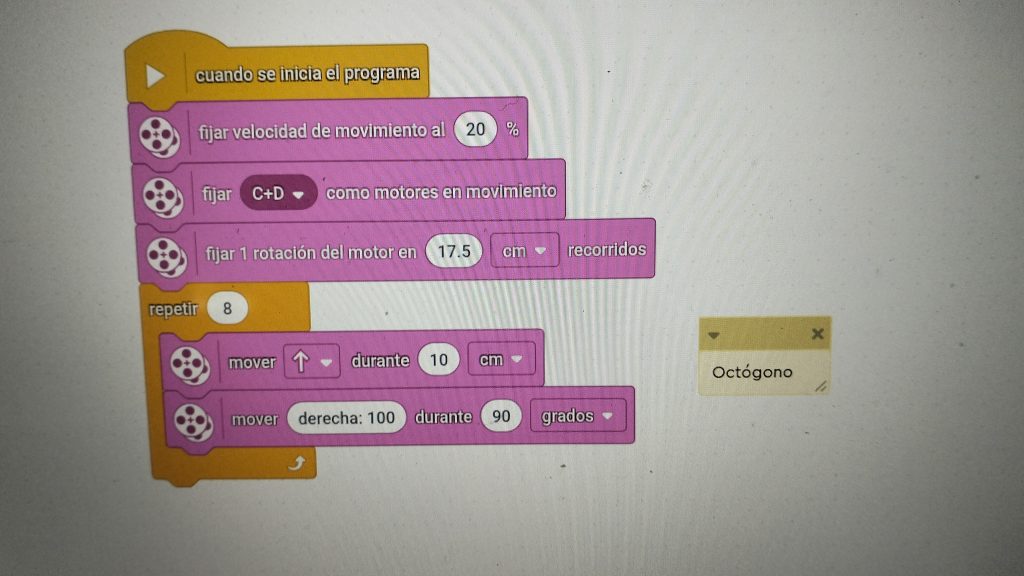
Dibujando un octógono
Ya nos debe salir solos, pero vamos a realizar la última operación: 360º/8 = 45º. 45º x 2 = 90º

Circunferencia
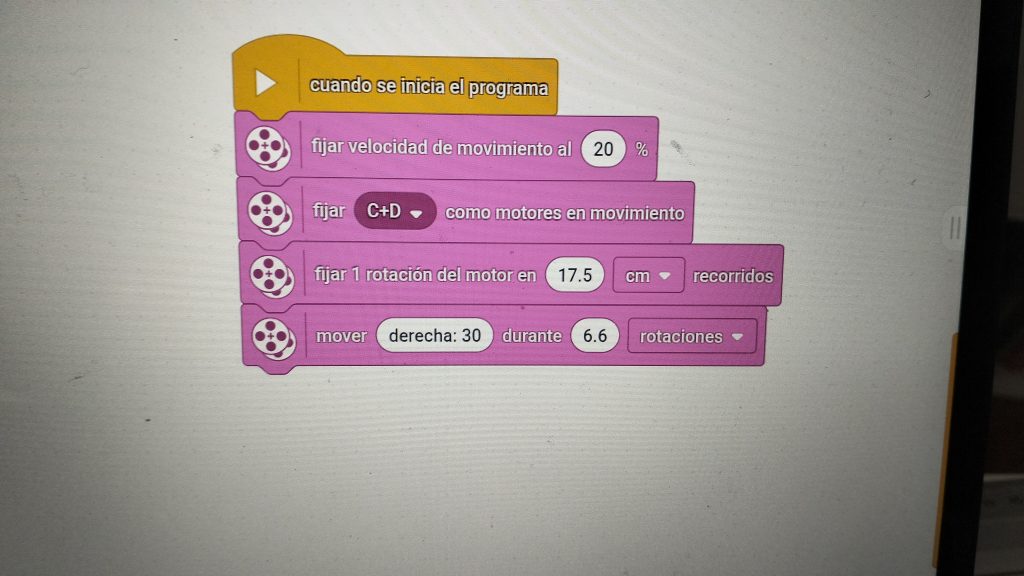
Aunque no es un polígono regular, si es una figura plana, así que también la vamos a incluir. Aqui jugamos con el desplazamiento del centro de giro. Si con 100, el robot gira sobre si mismo, otro número menor, va desplazando el eje de giro fuera del robot. En este caso hemos puesto 30 para que haga un círculo más grande. Estas medidas debemos ir ajustándolas tambien si cambiamos la circunferencia de las ruedas (ponemos ruedas más pequeñas o más grandes) o si aumentamos o disminuimos la distancia entre ellas.

Falta el triángulo equilátero. ¿Te atreves a hacerlo tu?. Espero que te haya sido divertido.
Quieres ver los robots en movimiento: Pica en el video
Do you want to see the robots moving: Click on the video
No tienes robots de Lego Spike
No hay problema. Con este simulador puedes hacer lo mismo, pero con robots online simulados.
Programación
Falta la hoja para la toma de datos y anotaciones de equipo que lleva toda Secuencia de Aprendizaje. De momento no está publicada.
English
I’m presenting a learning activity for you to use in the classroom with your students. For this activity, we’ve designed a special robot that draws lines on a whiteboard. It can also be used on paper once the design is complete.
By adapting the explanations and the level of difficulty, this activity can be used from 5th grade through 8th grade
This robot has the unique feature of holding a 12mm diameter marker between its front wheels. As the robot moves forward, it draws. The marker must be free-floating; that is, the robot only holds it upright, but it must be able to move vertically so it can draw.
Drawing a Square
Let’s imagine the figures as roundabouts. The robot must make the outer turn, like a car changing lanes, so the turning angle isn’t the angle of the figure itself, but its supplementary angle.
In geometric figures, the sums of their angles must equal (n – 2) x 180º, but we’re not looking for the interior angle, but rather its supplementary angle.
The supplementary angle of a square (which has 4 sides) would be: 360º/4 sides = 90º.
We remind our students that the turning angle of a motor (of a wheel) is not the same as the turning angle of a complete robot. Each wheel has a turning angle. In this case, one wheel moves forward 90º and the other another 90º, so we add 90 + 90 = 180º. This is what we put in our code.
Drawing a Pentagon
To calculate the supplementary angles of a pentagon, which has 5 sides, we would do this: 360º/5 sides = 72º. Since we have to turn 2 wheels, we double that amount: 72º x 2 = 144º.
Drawing an Hexagon
A hexagon has 6 sides. Following what we’ve learned, we simply perform the operation 360º / 6 sides = 60º. Since there are two motors, we must use 60º x 2 = 120º.
Drawing an Heptagon
In this figure it gets a little more complicated, since the division is not exact: 360º / 7 = 51.42º. Multiplying by 2 gives us 102.85º
Drawing an Octogon
We should be able to figure it out automatically now, but let’s do the last operation: 360º/8 = 45º. 45º x 2 = 90º
Drawing a Circunference
Although it’s not a regular polygon, it is a flat shape, so we’ll include it as well. Here we’re playing with the displacement of the center of rotation. If 100 makes the robot rotate on its own axis, a smaller number shifts the axis of rotation away from the robot. In this case, we’ve set it to 30 so it makes a larger circle. We’ll also need to adjust these measurements if we change the circumference of the wheels (using smaller or larger wheels) or if we increase or decrease the distance between them.
Triangle
The equilateral triangle is missing. Do you dare to draw it yourself? I hope you enjoyed it.
You don’t have Lego Spike robots
No problem. With this simulator, you can do the same thing, but with simulated online robots.
Programming
The data collection and team note sheet, which is included in every Learning Unit, is missing. It has not yet been published.